Nonlinear Dynamics: Logistic Model of Population Evolution

A simple quadratic equation (a parabola) can lead to a variety of behaviors when used in a finite-difference equation. The equation

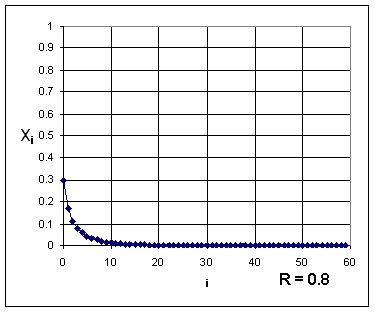
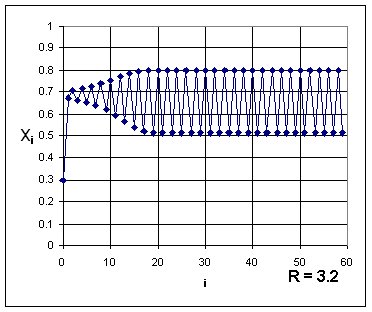
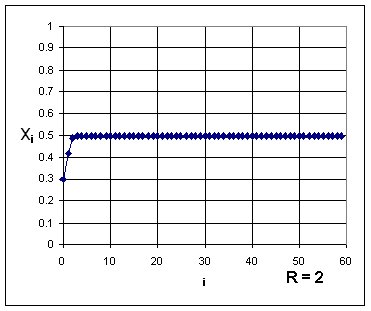
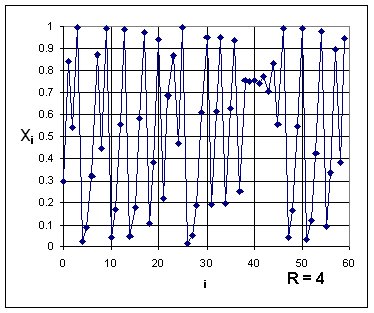
xi+1 = Rxi (1 - xi)

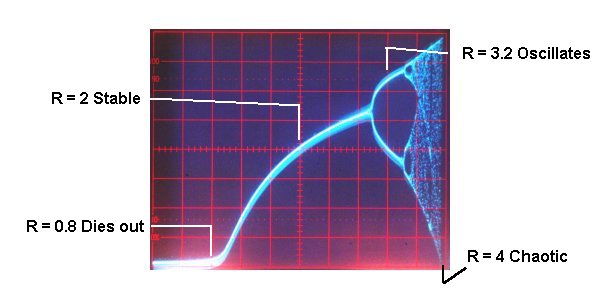
is known as the Logistic equation and is a model for population evolution. Depending on the value of R the population either dies out, is stable, oscillates periodically, or fluctuates chaotically. Examples are shown below. All possible behaviors can be displayed on a bifurcation diagram.

The bifurcation diagram on the oscilloscope shown below is from an electrical circuit that performs an analog computation of the Logistic equation while a voltage representing the parameter R increases from 0 to 4 volts . The behaviors shown in the 4 graphs below can be located on the bifurcation diagram.