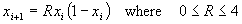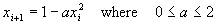Non-linear Dynamics
Chaotic Systems
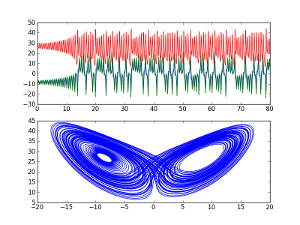
Real-time bifurcation diagrams produced from analog electronic circuits. Simple quadratic equations used in finite-difference recursion relations display a wide variety of behaviors including chaos.
Click for article (pdf) or Edward H. Hellen, Am. J. Phys. 72, 499(2004).
Hénon Equation (1-dim) |
Control of chaos
|
Deterministic chaos (as produced by the above examples) can be controlled by small perturbations of a system parameter (R or a). We derive the transient response for chaos control based on the first difference of the system variable, (xn − xn-1), and verify it experimentally. Graph shows measurements of system values and control parameter taken from controlled Hénon electronic circuit. Close-up of bifurcation data recorded from Keith's Hénon circuit. Shows period doubling from 4 to 8, period-3, period-5, and period-6 regions. |
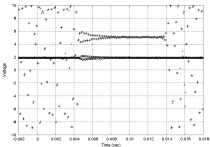 |
|
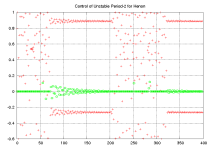
In addition to stabilizing a single fixed point, it is also possible to stabilize unstable periodic orbits. Here we show numerical simulation of control of Period-2 oscillation. System values are red. Perturbations to control parameter are green. Control was turned on at 50, off at 200, back on at 250. |
 |
Excitable Systems
|
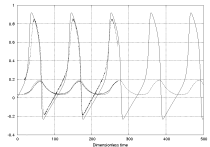
Fitzhugh-Nagumo. Here are a couple of VPython avi movies. Fitzhugh-Nagumo1 (shows phase-space), Fitzhugh-Nagumo2 (shows phase-space and time evolution). The system includes both a steady leakage current and a pulsed stimulation. Here is a spatiotemporal version showing propagation of excitations too close together: Fitz-Nag_Diffusion Modeling Excitable Systems: Reentrant Tachycardia AJP 78, 56(2010) J.L. Lancaster, E.M. Leise, and E.H. Hellen or pdf. Describes electronic and mathematical models, used to model a cardiac arrhythmia and its treatment. Here is SPICE prediction for the 3-transistor circuit. Uses Ebers-Moll model of npn transistor. |
 |
Genetic Network Modeling
Synthetic genetic networks can be constructed to perform desired functions. We explore potential dynamics of these networks by using numerical and electronic models.
Hellen, Edward H.; Dana, Syamal K.; Kurths, Juergen; Kehler*, Elizabeth; Sinha, Sudeshna. (2013) Noise-Aided Logic in an Electronic Analog of Synthetic Genetic Networks. PLOS ONE Volume: 8 Issue: 10 Article Number: e76032 Published: OCT 4 2013 10.1371/journal.pone.0076032
Hellen, Edward H.; Dana, Syamal K.; Zhurov, Boris; Volkov, Evgeny. (2013) Electronic Implementation of a Repressilator with Quorum Sensing Feedback. PLOS ONE Volume: 8 Issue: 5 Article Number: e62997 Published: MAY 2 2013 10.1371/journal.pone.0062997
Hellen EH, Volkov E, Kurths J, Dana SK (2011) An Electronic Analog of Synthetic Genetic Networks. PLoS ONE 6(8): e23286. doi:10.1371/journal.pone.0023286 10.1371/journal.pone.0023286
| α = 176, n = 4.1 β ratio = 0.45:0.1:0.1 k0 = 1, k1 = 0.01 η = 2, κ ≈ 10 Q varied |
|
α = 176, n = 4.1 β ratio = 0.45:0.1:0.1 k0 = 1, k1 = 0.01 η = 2, κ ≈ 10 Q = 0.23 | |
| α ≈ 88, n ≈ 2.5+ β's = 0.1 k0 = 1, k1 = 0.025 η = 2, κ increasesQ = 0 | α ≈ 88, n ≈ 2.5 β's = 0.1 k0 = 1, k1 = 0.025 η = 2, κ increasesQ = 0 |
|
Nonlinear Damping of the LC Circuit using Anti-parallel Diodes
Interesting amplitude
dependent behavior occurs when anti-parallel diodes replace the resistor in
a RLC circuit. The circuit becomes a nonlinearly damped harmonic oscillator
obeying the equation:
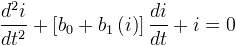 |
where | 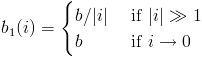 |
More info. or get article Hellen and Lanctot, Am. J. Phys. 75, 326(2007) Or click for pdf
Logarithmic Decay
Diode-capacitor circuit. What happens when the resistor in an RC decay circuit is replaced by a diode? The decay changes from exponential to logarithmic. (At least to a good approximation for 5 decades of time.)
Click for more on Diode-Capacitor Decay. For reprint of article, Click here (pdf) or, this article may also be found at Edward H. Hellen, Am. J. Phys. 71, 797(2003).
Padé-Laplace Curve-Fitting and Signal Averaging
Pade-Laplace is an intriguing method for finding the decay constants in a multi-exponential decay. Unlike standard methods of curve-fitting, it does not use the sum of the square of the errors and does not assume the number of decay constants. Instead it uses Laplace transforms, Pade approximants, Taylor series expansion, matrix inversion, and finding the zeroes of polynomials in order to determine the number of decay constants, their values, and their amplitudes. How it works
Here Padé-Laplace analysis is used on signal averaged data obtained from a simple circuit that produces multi-exponential voltage decays in the presence of noise. Click for article (pdf) or Edward H. Hellen, Am. J. Phys. 73, 871(2005).